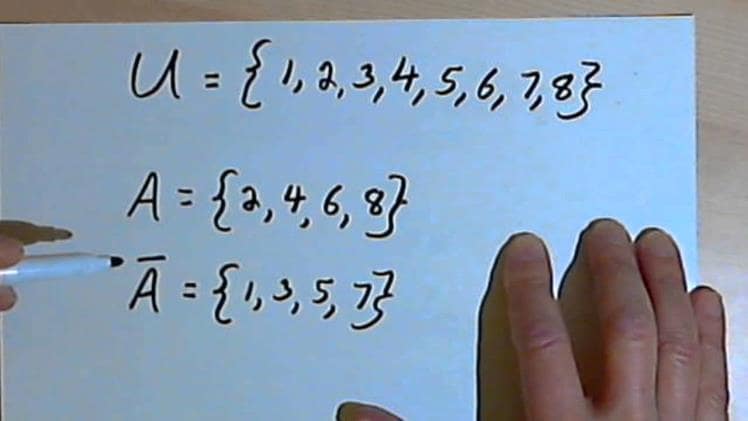In mathematics, we perform operations such as addition, subtraction, multiplication, and others on two or more numbers to obtain a resultant value. Similarly, in set theory, certain operations are performed on two or more sets to obtain a combination of elements, depending on the operation. There are four major types of operations on sets in set theory, such as:
- Union of Sets
- Intersection of Sets
- Difference of Sets
- Complement of a Set
On that note, let’s discuss these operations two at a time thoroughly, here Intersection and Complement of sets, for a better understanding.
Intersection of Sets
The set that contains all common elements from both sets A and B is called a set intersection. The phrase “AND” is used to indicate the Intersection of Sets, implying that the elements in the intersection are present in both A and B. The Intersection of the set is represented by the symbol “∩”. If x ∈A ∩B, then x∈A and x∈B, according to the standard definition.
Consider two friends throwing a party and only inviting their mutual pals. They typed their friends’ names into a spreadsheet, then searched for mutual friends and invited only those; this is known as the Intersection of the set of friends.
Intersection of Sets Properties
The Intersection Operation has the following properties:
- Commutative law: The intersection of two or more sets is governed by the commutative law, which states that if we have two sets A and B, then
A ∩ B = B ∩ A
- Associative law: The intersection operation is governed by the associative law, which states that if we have three sets A, B, and C, then
A ∩ (B ∩ C)= (A ∩ B) ∩ C
- Law of φ and U: In intersection, we get all common elements between two sets. There will be no common elements between φ and A since φ has no elements.
Therefore, the intersection of φ and A is φ.
φ ∩ A = φ
Similarly, the common elements between U and A will be all elements of A since U has all the elements.
Therefore, A is the intersection of U and A.
U ∩ A = A
- Distributive law:
A ∩ (B U C) = (A ∩ B) U (A ∩ C), i. e., ∩ distributes over U.
Complement of a Set
If “U” is a universal set and “A” is any subset of “U,” the complement of “A” is the set of all elements of “U” which are not elements of “A.”
A’ = {x:x ∈U and x∉A}.
Complement of a Set Examples
Consider a universal set “U” of all natural numbers less than or equal to 20 to make it more clear.
Let us define set A, which is a subset of U, as the set containing all prime numbers.
Thus we can see that,
A = {2,3,5,7,11,13,17,19}
All of the elements that are present in the universal set U but not in A make up the complement of this set A.
Therefore, A’ is given by:
A’={1,4,6,8,9,10,12,14,15,16,18,20}
Properties of Complement of Set
The complement of a set has three important properties. Let’s go over the three properties of a set’s complement:
Complement Laws: This property states that the union of two sets, A and A’, yields the universal set U, of which A and A’ are subsets.
A ∪ A’ equals U
In addition, the intersection of a set A and its counterpart A’ yields the empty set denoted by∅.
A ∩ A’ = ∅
Law of Double Complementation: This is the second of three properties of a set’s complement. If we take the complement of the complemented set named A’, we get the set A itself, according to the law of Double Complementation.
(A’ )’ equals A
Law of Universal Set and Empty Set: According to this law, the complement of the universal set gives us the empty set and vice versa.,
∅’ equals U And U equals ∅’.